frontop137's blog

分享技术与生活

0%

《算法图解》笔记

发表于 更新于 分类于

写在开头

最近读论文读累了总想找点其他事情做，知乎上推荐了一本《算法图解》，比较适合之前没有接触过算法的人入门，内容很少，读起来很轻松，茶余饭后读的话大概读2天就能读完。以下是这本书的读书笔记和里面一些算法的实现。

第一章：算法简介

仅当列表是有序的时候，二分查找才管用。时间复杂度为O(logn)

1
2
3
4
5
6
7
8
9
10
11
12
13
# 二分查找代码
def binary_search(in_list, num):
 left = 0
 right = len(in_list)-1
 while left <= right:
     mid = (left+right)//2
     if num == in_list[mid]:
         return mid
     elif num < in_list[mid]:
         right = mid - 1
     else:
         left = mid + 1
 return None

第二章：选择排序

  • 数组的优势：

    需要随机地读取元素时，数组的效率很高，因为可迅速找到数组的任何元素。

  • 链表的优势：

    链表的优势在插入元素方面

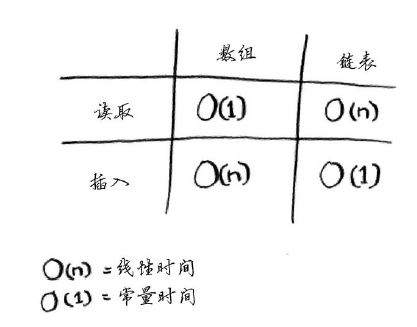
需要同时读取所有元素时，链表的效率很高，但如果需要跳跃时，链表的效率很低。

1.png

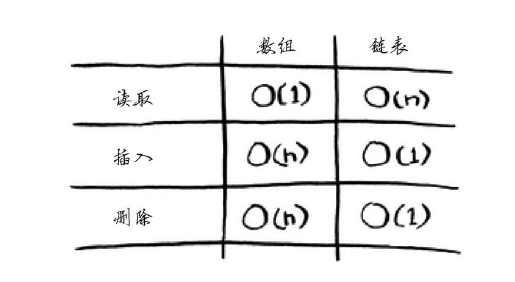
数组和链表常见操作运行时间：

2.png

需要指出的是，仅当能够立即访问要删除的元素时，删除操作的运行时间才为O(1)。

链表只支持顺序访问，而数组不仅支持顺序访问，还支持随机访问。

选择排序时间复杂度O（$n^2$）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 选择排序算法
# 先编写选出最小元素的函数
def sel_small(arr):
 small = arr[0]
 small_idx = 0
 for i in range(1, len(arr)):
     if arr[i] < small:
         small_idx = i
 return small_idx


# 再编写选择排序算法
def selection_sort(arr):
 result = []
 while arr:
     small_idx = sel_small(arr)
     result.append(arr.pop(small_idx))
 return result

第三章：递归

递归只是让解决方案更清晰，并没有性能上的提升。如果使用循环，程序的性能可能更高；如果使用递归，程序可能更容易理解。

每个递归函数都有两部分：基线条件（base case）和递归条件（recursive case）。基线条件指函数不再调用自己，从而避免形成无限循环，递归条件指函数调用自己。

所有函数的调用都直接入栈。

1
2
3
4
5
6
# 阶乘函数
def fact(n):
 if n == 1:
     return 1
 else:
     return n*fact(n-1)

第四章 快速排序

使用分治算法（D&C，divide & conquer）需要包含的步骤：

分土地问题

  • 找出基线条件，这种条件必须尽可能简单
  • 不断将问题分解（或者说缩小规模），直到符合基线条件

D&C并非可用于解决问题的算法，而是一种解决问题的思路。

  • 快速排序

    平均（最佳）时间复杂度O(n·logn)，最糟糕的情况时间复杂度为$O(n^2)$。快速排序的性能高度依赖于你选择的基准值。其中，平均情况即随机选择一个pivot，这时栈的纵向时间长度为$O(\log n)$，横向时间一直为$O(n)$，最差的情况是选择的pivot不是最大就是最小，这时总有一个空列表，这时栈的纵向时间长度为$O(n)$,横向长度同样一直为$O(n)$，因此总的时间复杂度为$O(n^2)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 计算列表的和
def sum_arr(arr):
if not arr:
   return 0
elif len(arr) == 1:
   return arr[0]
else:
   return arr[0] + sum_arr(arr[1:])


# 计算列表元素个数
def count_arr(arr):
if not arr:
   return 0
else:
   return 1+count_arr(arr[1:])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 快速排序
def quick_sort(arr):
 if len(arr) <= 1:
     return arr
 if len(arr) == 2:
     if arr[0] <= arr[1]:
         return arr
     else:
         return arr[::-1]
 else:
     pivot = arr[0]
     less = [i for i in arr[1:] if i < pivot]
     greater = [i for i in arr[1:] if i >= pivot]
     return quick_sort(less)+[pivot]+quick_sort(greater)

第五章：散列表（哈希表）

1.png

  • 冲突：给两个键分配的位置相同。处理冲突的方式很多，最简单的办法如下：如果两个键映射到了同一个位置，就在这个位置存储一个链表。

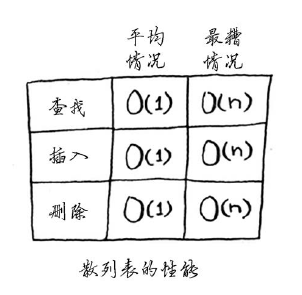
散列表的性能：

2.png

在最糟情况下，散列表所有操作的运行时间都为O(n)——线性时间。

为了避免冲突，要求：

  • 较低的填装因子。
  • 良好的散列函数。良好的散列函数让数组中的值呈均匀分布，糟糕的散列函数让值扎堆，导致大量的冲突。

第六章：广度优先搜索

解决最短路径问题的算法被称为广度优先搜索。广度优先搜索是一种用于图的查找算法。

考虑水经销商的问题！

广度优先算法可解决两类问题：

  • 从A节点出发，可以到达B节点吗？
  • 从A节点出发，前往节点B的那条路径最短？

广度优先搜索不仅查找从A到B的路径，而且找到的是最短的路径。

应用广度优先时应该用队列将每一个一级节点的子节点存入队列中。并且已经遍历过的节点不能再次遍历，这样会无限循环下去。

广度优先搜索的运行时间为O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 关系网
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []

from collections import deque


# 判断一个人是否为芒果经销商
def person_is_seller(name):
 return name[-1] == 'm'


# 广度优先搜索
def bfs_search(graph):
 searched = []  # 用于装已经被检查过的人
 search_queue = deque()
 search_queue += graph['you']
 while search_queue:
     name = search_queue.popleft()
     if name not in searched:
         if person_is_seller(name):
             print(name)
             return
         else:
             search_queue += graph[name]

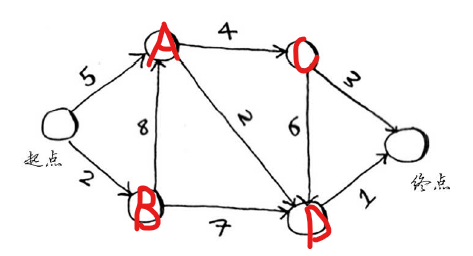
第七章：狄克斯特拉算法

狄克斯特拉算法包含4个步骤：

  • 找出“最便宜”的节点，即可在最短时间内到达的节点。
  • 更新该节点的邻居的开销，其含义将稍后介绍。
  • 重复这个过程，直到对图中的每个节点都这样做了。
  • 计算最终路径。

要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。

狄克斯特拉算法只适用于有向无环图（directed acyclic graph，DAG）。

换钢琴实例

如果有负权边，就不能使用狄克斯特拉算法！原因：对于处理过的海报节点，没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。

1.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# Dijkstra算法

import math
# 图字典
graph = dict()
graph['start'] = {}
graph['start']['a'] = 5
graph['start']['b'] = 2
graph['a'] = {}
graph['a']['c'] = 4
graph['a']['d'] = 2
graph['b'] = {}
graph['b']['a'] = 8
graph['b']['d'] = 7
graph['c'] = {}
graph['c']['d'] = 6
graph['c']['finish'] = 3
graph['d'] = {}
graph['d']['finish'] = 1
graph['finish'] = {}

# 代价字典
cost = dict()
cost['a'] = 5
cost['b'] = 2
cost['c'] = math.inf
cost['d'] = math.inf
cost['finish'] = math.inf

# 父节点字典
father = dict()
father['a'] = 'start'
father['b'] = 'start'
father['c'] = None
father['d'] = None
father['finish'] = None


def dijk(graph, cost, father):
 processed = []
 while len(processed) < len(cost.keys()):
     # 找到cost字典中的最小值，其中之前找过的不再使用
     node_cost = math.inf
     node = 'finish'
     for key, value in cost.items():
         if key not in processed:
             if value < node_cost:
                 node_cost = value
                 node = key
     processed.append(node)
     for key, value in graph[node].items():
         if value+node_cost < cost[key]:
             cost[key] = value + node_cost  # 更新cost表
             father[key] = node  # 更新父亲节点
 # 路径
 temp = 'finish'
 path = 'finish'
 while temp != 'start':
     temp = father[temp]
     path = temp + '->' + path
 print('路径：', path)

 return cost['finish']

# 运行：
if __name__ == '__main__':
 print('最短距离：', dijk(graph, cost, father))
# 运行结果：
路径： start->a->d->finish
最短距离： 8

第八章：贪婪算法

贪婪算法很简单：每步都采取最优的做法！每步都选择局部最优解，最终得到的就是全局最优解。

评判近似算法的标准：

  • 速度有多快
  • 得到的近似解与最优解的接近程度。

集合覆盖问题~NP完全问题

面对NP完全问题，无法找到最优解，所以采用近似算法。

1.png

贪婪算法就是一种简单的近似算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 广播台分配问题(集合覆盖问题)

# 需要覆盖的州
states_needed = {"mt", "wa", "or", "id", "nv", "ut", "ca", "az"}
# 广播台对应字典
stations = dict()
stations["kone"] = {"id", "nv", "ut"}
stations["ktwo"] = {"wa", "id", "mt"}
stations["kthree"] = {"or", "nv", "ca"}
stations["kfour"] = {"nv", "ut"}
stations["kfive"] = {"ca", "az"}


def station_schedule(states_need, stations):
 covered = set()
 greedy = None
 chosen = set()
 while covered != states_needed:
     covered_num = 0
     for key, value in stations.items():
         if len(value-(value & covered)) > covered_num:
             covered_num = len(value-(value & covered))
             greedy = key
     covered = covered | stations[greedy] - (stations[greedy] & covered)
     chosen.add(greedy)
     del stations[greedy]
 return chosen

# 运行
if __name__ == '__main__':
 print(station_schedule(states_needed, stations))

# 运行结果：
{'kone', 'kfive', 'ktwo', 'kthree'}

第九章：动态规划

动态规划先解决子问题，再逐步解决大问题。

首先分析背包问题：

余下了空间时，你可根据这些子问题的答案来确定余下的空间可装入哪些商品。

动态规划基本公式！！！

2.png

接下来分析旅游行程最优化问题

动态规划功能强大，它能够解决子问题并使用这些答案来解决大问题。但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。

动态规划启示：

  • 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
  • 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。要设计出动态规划解决方案可能很难，这正是本节要介绍的。下面是一些通用的小贴士。
  • 每种动态规划解决方案都涉及网格。
  • 单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。
  • 每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴。

本书一共11章，第10章粗浅介绍了机器学习，第11章介绍了以后的学习方向，这里就不做笔记了。

最后附上本书PDF链接，有兴趣的同学可以自取：

点击下载pdf文件