背景
隐马尔可夫模型(Hidden Markov Model, HMM)是可用于标注问题的统计学习模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型。
在统计学的贝叶斯学派衍生的概率图模型中,在模型中加上时间这一测度,就产生了动态模型(Dynamic Model),动态模型又根据隐变量的离散与否和状态和输出是否满足高斯分布而分为隐马尔可夫模型、卡曼滤波和粒子滤波,其中马尔可夫模型的隐变量(隐状态)是离散的:
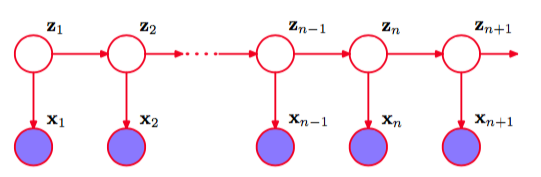
模型简介
其中,$\pi$表示初始状态概率,A表示状态转移矩阵,B表示发射矩阵(固定状态后观测值的概率)。
模型的基本符号表达与定义:
关键的两个假设:
隐马尔可夫模型满足两个很关键的假设,第一是模型满足齐次马尔可夫性(Markov Property),即当前时刻的状态只跟上一时刻的状态有关:第二个假设是模型满足观测独立性,即当前时刻的输出只和当前时刻的状态有关,与之前时刻的状态无关:
以上两个假设是在整个HMM推导中要反复用到的关键条件。
HMM要解决的三个主要问题:
- 概率计算问题(Evaluation):
计算$P(O|\lambda)$,我们采用前向算法(Foward Algorithm)和后向算法(Backward Algorithm)。 - 学习问题(Learning):
求$\lambda$,我们采用Baum-Welch算法(即EM算法)。 - 预测问题(又称编码问题,Decoding):
计算$I=\mathop{\arg\max}_iP(I|O)$,我们采用维特比算法(Viterbi Algorithm)。
- 概率计算问题(Evaluation):
Evaluation问题
首先,通过添加随机变量然后再求积分消去(很常规的方法),构造联合条件概率$P(O,I|\lambda)$:
分别利用之前提到的两个假设求出$P(O|I,\lambda)$和$P(I|\lambda)$,但是这样会造成很大的计算复杂度(唯独诅咒),于是我们只能联想用递推的方式求解:
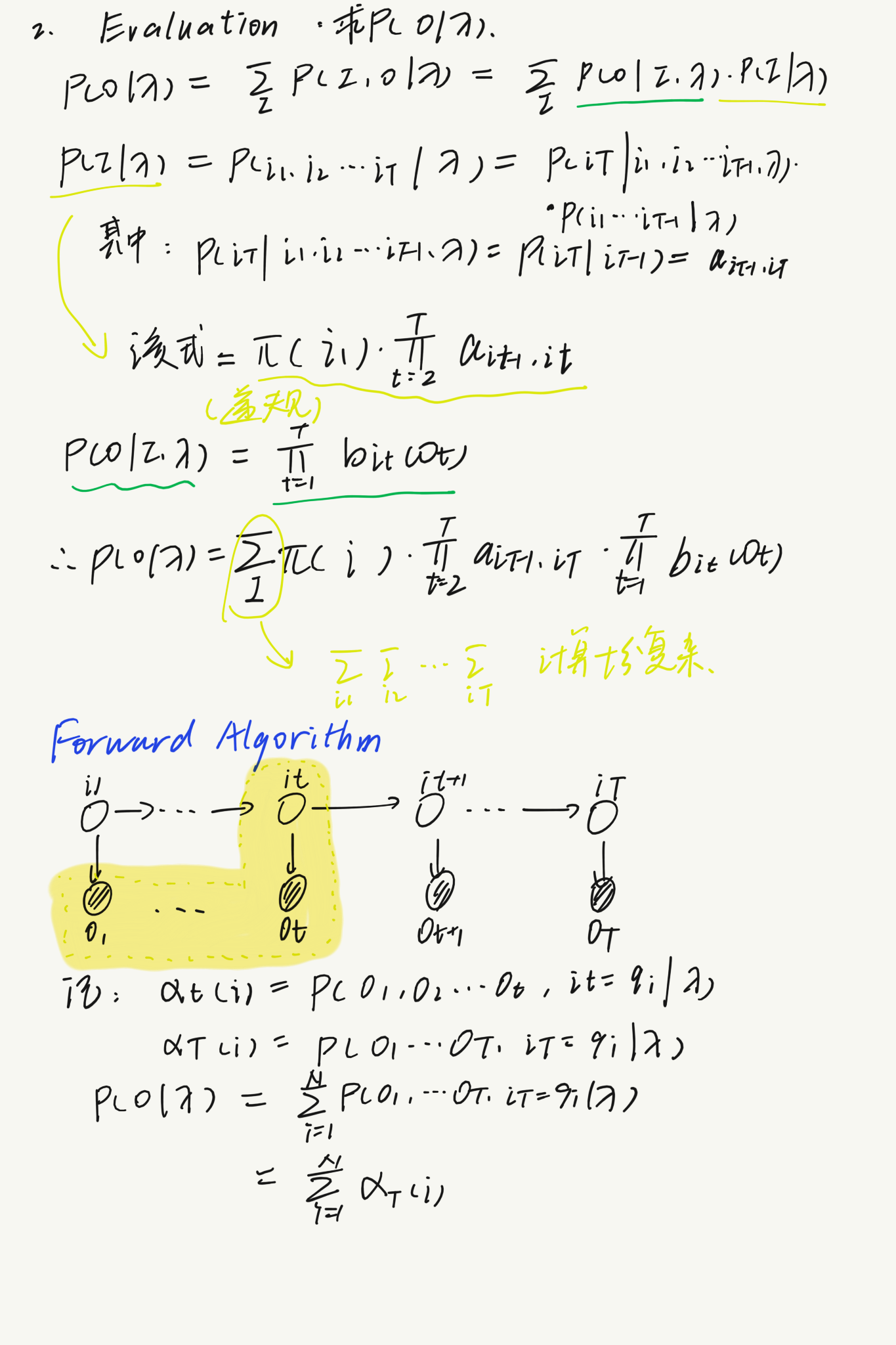


利用前向算法和后向算法,成功构造出了递推关系,可以较为方便地求解观测序列的输出概率。
Learning问题
已知观测序列O,求解模型的参数$\lambda$。因为状态序列是潜在的(隐藏的),是不可以观测到的,所以就很自然的令我们想到了EM算法(实际上为了解决HMM中的Learning问题而提出Baum-Welch算法时还没有EM算法,EM算法是后期对这一类算法做了归纳和整理):
即我们只需要构造等式:
在HMM中,$\theta$为$\lambda$(参数),$z$为$I$(隐变量),$x$为$O$(观测变量):


这里只求出了$\pi$(在目标函数中只要取第一项即可,因此计算比较简便),A和B的计算过程太过复杂,这里不予展示,但是思路相同。
Decoding问题
若时间序列长度为T,共有N种状态,则全部的马尔科夫链的状态序列有$N^T$种,我们的目的就是从这么多种序列中挑出一个,使得后验概率达到最大(即一个路径动态规划问题)。
我们首先要明确的一点是,假设在时间t时我们已经确定了一个能使之前所有状态序列的后验概率达到最大的状态,那么t时刻之后的所有的部分路径必须达到最大(可采用反证法轻易证明)。那么我们定义到达某个特定状态$q_i$的概率为$\delta_t(i)$,取最大即为在t时刻状态出现在$q_i$的概率最大(i的取值即为t时刻的最佳状态),t时刻之前的可以忽略。接下来我们只需要找到递推式$\delta_{t+1}(j)$与$\delta_t(i)$之间的关系即可。
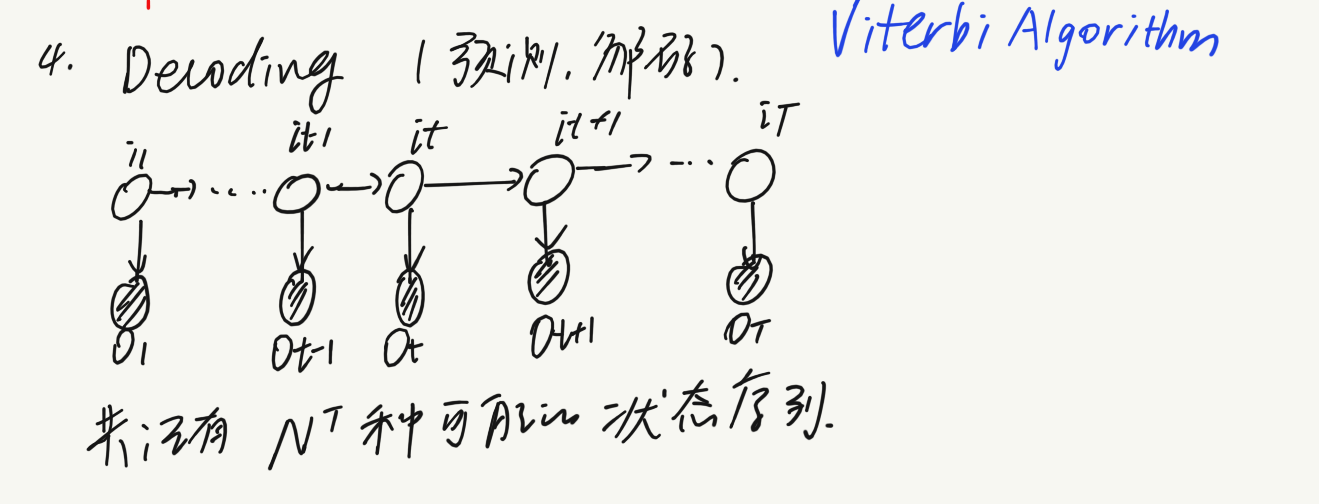

因此我们只需要从t=1开始,递推的计算在时刻t状态为i的各条部分路径的最大概率,直至得到时刻t=T状态为i的各条路径的最大概率,此时的概率即为最优路径的概率,T时刻最优的状态也就可以确定。然后再从后向前不断地找到每个时间点的最优状态。这就是维特比算法。
参考资料
[1].李航《统计机器学习》
[2].bilibili白板推导系列14