前段时间阅读了李航老师《统计机器学习》第9章“EM算法及其推广”,对EM算法有了初步的了解,对于EM迭代的思想有了初步的认识。这段时间又观看了徐亦达老师的“机器学习课程”视频中的“Expectation Maximization”,将EM框架和高斯混合模型做了更好地结合,这篇文章旨在做一个简单的总结,复习和巩固自己所学习的知识。
EM初探
EM算法,名称取自期望(Expectation)和最大值(Maximization)的首字母,是一种迭代算法,用于含有隐变量的概率模型的极大似然估计(或最大后验估计),我们在了解EM算法的流程之后,更重要的是验证其收敛性以及将EM算法与高斯混合模型结合(最常见)。在引入《统计学习方法》中经典的“三硬币模型”之前,我想换一个角度,来解释为什么我们需要使用EM算法:

以高斯模型为例,由上图可见,我们处理的数据往往不是一个高斯模型可以拟合的,这时我们需要多个高斯模型来拟合数据,假设有K个模型,每个高斯模型需要确定2个参数($\mu, \sigma$),每个模型前还需要有一个权重($\alpha$),故描述这些数据共需要(K+K+K-1=3K-1)个参数($\alpha$参数存在约束,故只需要K-1个):
我们只需要对这3K-1个参数分别求偏导,并令偏导数等于零,就可以确定模型参数,但是首先,求导很复杂,其次令偏导数等于零,求解这个方程组更加复杂。于是我们想到了要用迭代的方法,一次一次的逼近,每次迭代求出的$\theta$代入似然函数都比之前的增大,这样最终得到的$\theta$即为我们的估计参数。这也就是EM算法。
EM算法推导
既然是迭代算法,就首先需要建立迭代前后的关系式:
在EM算法中,我们定义的迭代关系式为:
Z即为我们引入的隐变量(辅助变量),Z取值为1~K,分别对应K个高斯分布模型,这样实际我们只需要用到一个高斯分布,大大简化了计算量。之前也讲过,迭代的目的是生成使似然函数不断增大的$\theta$ ,即必须保证:
接下来我们来证明我们所确定的迭代关系式如何能完成迭代的功能:
对两边同时求期望:
等式左边等于:
等式右边等于:
令右边的式子等于:
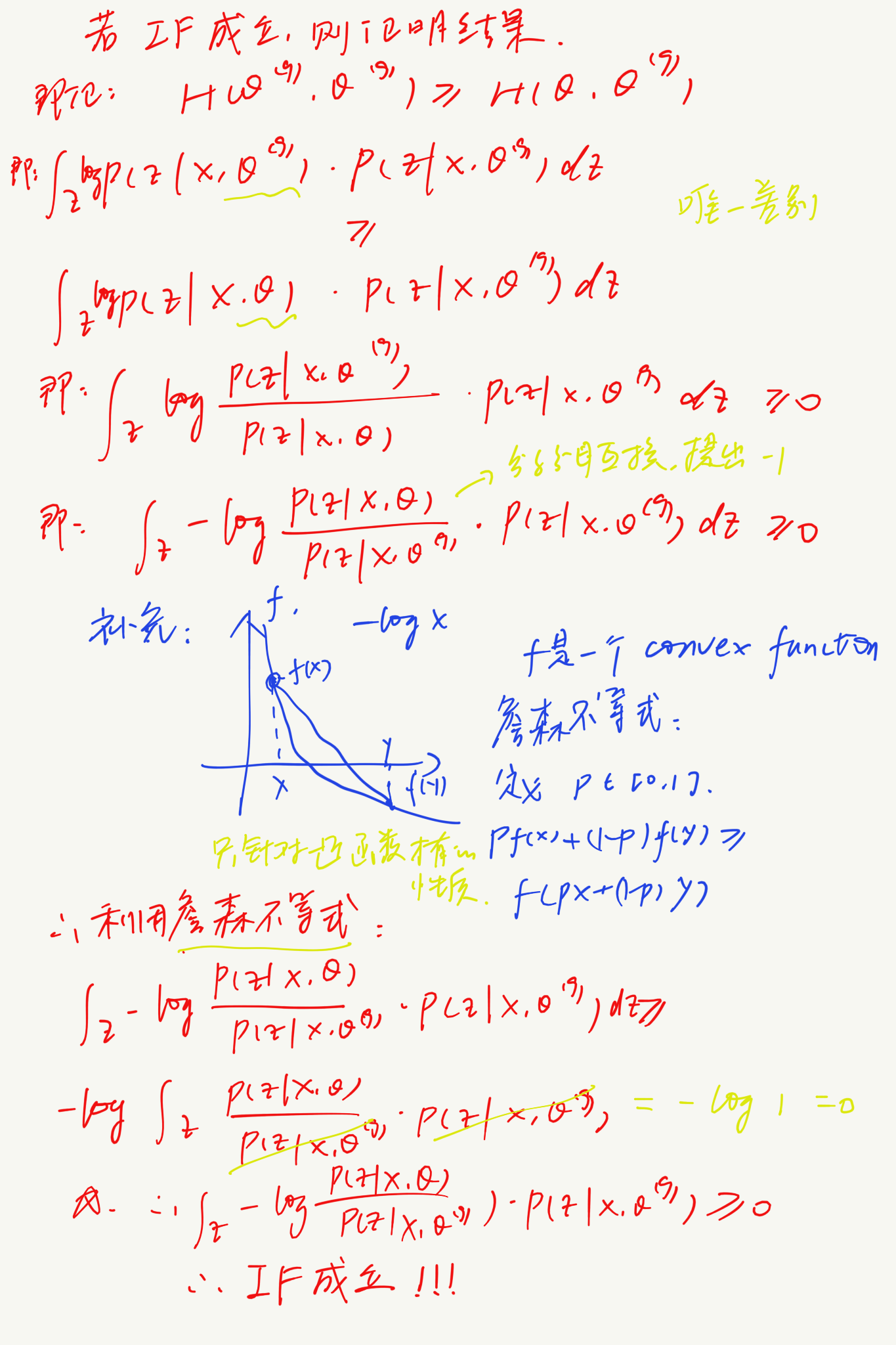
可以清楚地看出,Q函数为我们迭代的一项,即迭代过后:$Q(\theta^{g+1},\theta^g)>Q(\theta,\theta^g)$;故此时我们只需要证明H函数在迭代之后变小,就可以证明右边的式子在迭代后整体变大了(被减数增大,减数减小),从而证明左式在迭代后增大。我们应用Jenson不等式来证明H减小:

EM框架下的高斯混合模型
N为样本总数,K为模型总数。
其中$P(z_i|\theta)$为每个模型的权重$\alpha_z$,$P(x_i|z_i,\theta)$为高斯分布的概率密度函数$N(\mu_{zi},\sigma_{zi})$。
- E-STEP
其中,$f_1(z_1)=log\alpha_z+logN(\mu_{z_1},\sigma_{z_1})$
上式即为似然函数求完期望的结果,接下来只需要最大化(argmax),分别求出三个参数$\alpha,\mu,\sigma$
- M-STEP
以求$\alpha$为例:
$\mu和\sigma$以相同的方式求出。
总结
EM算法为我们求解似然函数最值提供了一种有效的简便的算法,主要应用在含有隐变量的概率模型的学习。构建具体的EM算法时,最重要的是确定Q函数,每次迭代过程,EM算法通过最大化Q函数的值来增大对数似然函数。
由于本篇博文是第一次在hexo上面用latex写公式,hexo对于markdown和latex的渲染有很多冲突和问题,到现在我还没有完全解决,所以本文公式基本都是最简的,省去了很多的化简部分以及说明,并且主要是基于徐亦达老师的视频推导,而《统计学习方法》从“三硬币模型”入手,同时伴有大量的数学推导,可以帮助大家更加全面和严谨地了解EM算法,大家如果想更加详细的了解EM算法及其衍生算法,推荐还是先研读李航老师的《统计机器学习》。
参考资料
[1].李航,《统计机器学习》
[2].b站徐亦达机器学习课程